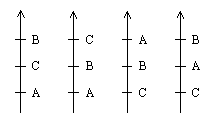
The diagram below shows an election where 52 voters ranked three
candidates.
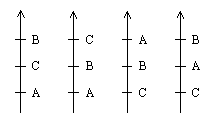
Each voter has indicated his/her preferences, and the "arrow"
on the left is interpreted to mean that 12 voters preferred B
to C, B to A and C to A. This notation can be extended to allow
voters who are indifferent between two or more candidates. (For
simplicity, for most of the discussion below we exclude elections
where voters are indifferent between two or more candidates.)
We can construct a matrix (table) to represent this election as follows: Label the rows and columns of the matrix with the candidates' names. The entry in the row labeled i and the column labeled j is the number of voters who preferred candidate i to candidate j.
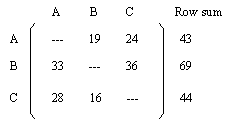
The row sums are of interest because they allow one to use the
vote matrix to compute the winner of a popular method of deciding
elections called the Borda Count. In the Borda Count candidates
are given credit in the form of points for how high up on a voter's
preference schedule a candidate appears. The number of points
a candidate would get would be the number of candidates below
him/her on the preference schedule. For example, to compute the
Borda Count for candidate B in the election above, starting with
the preference schedule which received 12 votes, B would get:
12 votes times 2 points + 16 votes times 1 point + 19 votes times
1 point + 5 votes times 2 points =
12(2) + 16(1) + 1(19) + 5(2) = 24 + 16 + 19 +
10 = 69.
Note that this is exactly the row sum of the second (B) row of
the vote matrix.
Problem
Given an election, it is simple to compute its vote matrix. However,
given a vote matrix, one can ask the question of whether or not
there is some election which gives rise to the vote matrix. The
problem is: given a vote matrix which is 3x3 with "blank
entries" on the diagonals, give an algorithm (mechanical
procedure) for constructing an election, if one exists, which
has the given matrix as its vote matrix.
Extensions
1. Consider the same question for matrices which arise from elections
where there are n (rather than 3) candidates.
2. Consider the problem when ties between candidates in the preference
schedules of individual voters are permitted.
References:
1. Garfunkel, S., (project director), For All Practical Purposes,
4th ed., W. H. Freeman, New York, 1997.
2. Malkevitch, J. and W. Meyer, Graphs, Models and Finite Mathematics,
Prentice-Hall, Englewood Cliffs, 1974.
3. Malkevitch, J. and G. Froelich, The Mathematical Theory of
Elections, COMAP, Lexington, 1988.
4. Straffin, P., Topics in the Theory of Voting, Birkhäuser
Boston, Boston, 1980.
Previous | Home | Glossary | Next