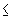 c({A})
b
c({A})
b 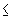 c({B})
c
c({B})
c 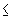 c({C})
c({C})
It often happens that when individuals (or towns or companies)
cooperate they can achieve savings over what costs would be if
they were to proceed on their own. Imagine that there are three
individuals A, B, and C and that if they do a certain project
on their own the cost to A, B, and C, respectively, would be:
If two of the individuals cooperate, there is a saving. The costs
to pairs of individuals when they cooperate are:
C({A,B}) = 22; C({A,C}) = 26; C({B,C}) = 30
When all three individuals cooperate the cost to the group is:
C({A,B,C}) = 34
Denote by a, b, and c the amount that is assigned as the cost
to each of A, B, and C respectively, when they cooperate as a
group of three. It would not make sense for A, B, and C to cooperate
unless the following conditions hold:
i. a 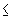 c({A})
b
c({A})
b 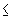 c({B})
c
c({B})
c 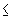 c({C})
c({C})
ii. a + b 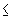 c({A,B}) b + c
c({A,B}) b + c 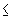 c({B,C}) a + c
c({B,C}) a + c  c({A,C})
c({A,C})
iii. a + b + c = c({A,B,C})
Unless these conditions all hold it would make not sense for the
players to cooperate together, since there would be an incentive
for the "grand coalition" to break up and be replaced
by a pattern where at least some of the players could achieve
lower costs for themselves at the expense of the other players.
Those values of a, b, and c which satisfy i., ii., and iii., constitute
the core of the game. Unfortunately, not all three-person
games have a core.
It is possible to draw a picture of the core (if there is a core)
of a 3-person game or to visualize why the game has no core. The
way to do this is to begin with an equilateral triangle of altitude
M, where M is the value that the grand coalition can achieve by
working together. Thus, the coordinates of each point in the triangle
correspond to a payoff to each of the three players A, B, and
C when they participate in the grand coalition.
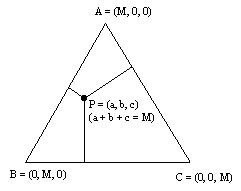
For each point in the triangle P, draw the lines from P perpendicular
to the sides of the triangle. The coordinates of P will be the
lengths of these segments. This follows from a theorem in Euclidean
geometry which states that in an equilateral triangle, for any
interior point of the triangle the sum of the three perpendicular
segments to the sides of the triangle sums to the length of the
altitude of the triangle.
The payoffs to the coalitions in the cost sharing game can be graphed in the diagram above. In the example above the fact that player A will not accept any cost more than 10 means that b + c = 24 and the fact that players B and C will not accept any cost more than 30 (b + c = 30) means that a = 4. In terms of the diagram we have a situation where to meet the conditions imposed we must choose a point that lies within a strip between two lines as shown.
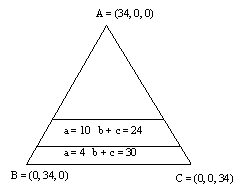
Note that side AB of the triangle satisfies: c = 0, a + b = 34;
side BC of the triangle satisfies: a = 0, b + c = 34; and side
AC of the triangle satisfies: b = 0, a + c = 34.
Any acceptable solution would have to lie between the two straight
lines shown. In a similar manner one can draw in the same diagram
the lines which correspond to the other rationality requirements
required of the core ((i), (ii), and (iii), above), and thereby
be able to see if a core exists or not.
Exercise:
a. Complete the diagram that is involved in the specific cost
sharing game under consideration.
b. Draw a different diagram for the situation when the cost values
to all the coalitions are the same except for the grand coalition,
which changes to 38 (i.e. instead of c({a,b,c}) = 38, c({a,b,c})
= 34).
Associated with this original situation involving sharing costs
is another "game" which involves the sharing of savings.
For each coalition one can compute the amount that this coalition
would save compared with the stand- alone costs for the individuals
that make up that coalition:
For example, if A and B work together the cost they incur is 22,
while if they work separately they incur costs adding to 26; thus
the cost saving by cooperating is 4. The savings involved to each
coalition are shown above, using the notation s standing for the
"saving" of each coalition. Note that in the cost allocation
context each player wants costs to be low, while in the savings
context each player looks for a larger cost saving.
We can draw a diagram of the savings game in the same manner that
we drew one for the original cost allocation situation. Again,
if the game has a core we will get a visual image of it by this
procedure.
Exercise
a. Draw the diagram associated with the cost saving game above,
associated with the original cost sharing game.
b. Draw the diagram associated with the cost savings game described
in Exercise b above.
Problem
a. Study the relationship between the diagram of the original
situation and the diagram of the cost saving game.
References:
1. Luce, R. and H. Raiffa, Games and Decisions, Wiley, New York,
1957, (reprinted by Dover Press).
2. Kahan, J. and A. Rapoport, Theories of Coalition Formation,
Lawrence Erlbaum Associates, Hillsdale, New Jersey, 1984.
3. Straffin, P., Games and Strategy, Mathematical Association
of America, Washington, 1993.
Previous | Home | Glossary | Next