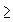1), no three
of which are collinear (i.e. lie on a straight line).
Suppose we are given 3n points in the plane (n 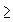1), no three
of which are collinear (i.e. lie on a straight line).
Problems
1. Is it possible to create from these points n triangles which
have no points in common (i.e. are disjoint)?
2. Given 6 points in the plane no three of which are collinear,
for what configuration(s) of the points is the number of ways
to form two disjoint triangles a maximum? a minimum?
3. If there is a configuration of 6 points for which one can select
k pairs of three points and form two disjoint triangles and another
6 point configuration for which one can select m pairs of three
points and form two disjoint triangles are there 6 point configurations
for which this can be done for each number which lies between
k and m?
3. How does the situation change if, instead of insisting that
the triangles formed have no points in common, we require that
the convex hulls of the triangles have no points in common?
Extensions
1. Extend Problem 2 to 9, 12, etc., points.
2. Generalize problem 3.
3. Generalize the problems above to (s)(n) points.
Previous | Home | Glossary | Next