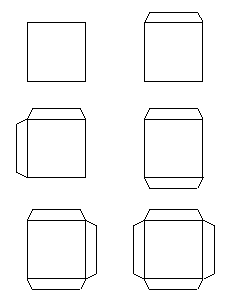
Figure 1
A 3-dimensional cube has six square faces and twelve edges. Marion
Walter (University of Oregon) observed that a cube can be assembled
in a variety of ways from square panels with tabs on which glue
can be applied. This project suggests how diophantine equations
(e.g. equations with non-negative integer solutions) can be used
to study this question and related questions in a systematic way,
while at the same time providing opportunity to learn some new
geometry. The accompanying Figure 1 show squares with 0, 1, 2,
(two types), 3 and 4 gluing tabs.
An interesting problem is to determine all the ways of assembling
a cube with such panels. To proceed in a systematic way let Xi
( i = 0, 1, 2, 3, 4 ) denote the number of panels with i tabs
which are used. Since the cube has six panels:
(1) X0 + X1 + X2 + X3 + X4 = 6.
Since the cube has 12 edges that must be glued:
(2) 0 X0 + 1X1 + 2X2 + 3X3 + 4X4 = 12.
Note that the assumption is being made that every edge of the
completed cube has exactly one pasted tab.
Problem
1. Choose one of the variables X1, X2, X3, X4 to
eliminate between
these two equations. Use this new diophantine equation to enumerate
all possible values of the Xi's that solve (1) and (2). (You may
wish to compare and contrast what happens when different choices
are made for which variable to eliminate.)
2. Corresponding to each possible solution of (1) and (2), can
one use panels of this type to construct a cube? (Remember that
for solutions involving X2 > 0, one can use two different
types of panels.)
3. Develop analogs to (1) and (2) for a cube with one face removed,
and answer the analog of Problem 2 for the "open" cube.
4. Develop analogs of equations (1) and (2) when the variable
X2 is replaced by X2' and X2'' and contrast what happens when
you try to deal with Problems 1-3 in this context.
Extensions:
1. Pose and solve the analog of the problems above for the (convex)
polyhedra that can be constructed with equilateral triangles.
(There are 8 such solids, the simplest being the tetrahedron (4
equilateral triangles), the bipyramid (6 equilateral triangles),
and the octahedron (8 equilateral triangles).
2. Pose and solve the analog of the problems above for the regular
dodecahedron, or for solids all of whose faces are congruent rhombuses,
or all of whose faces are regular polygons.
3. A net of a polyhedron is a planar pattern that can be folded
into the polyhedron. The cube, for example, has 11 nets. Examine
the issue of pasting tabs for nets of polyhedra such as the cube,
tetrahedron, etc.
References:
1. Beck, A., and M. Bleicher, and D. Crowe, Excursions into Mathematics,
Worth, New York.
2. Pearce, P. and S. Pearce, Polyhedra Primer, Van Nostrand Reinhold,
New York, 1978.
3. Walter, Marion, Boxes, Squares, and Other Things, NCTM, Reston,
1970.
Previous | Home | Glossary | Next