The Platonic solids (e.g. cube, tetrahedron, octahedron, dodecahedron,
and icosahedron) are very symmetric 3-dimensional polyhedra. The
purpose of this project is to explore the coloring of the faces
(see extensions) of these solids which takes account of their
structure and symmetry.
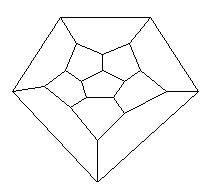
Let us take the dodecahedron as an example. This solid has 12
faces, 20 vertices, and 30 edges. Note that it is not necessary
to think of the dodecahedron as a solid in three-dimensional space
for the purpose of this investigation but in terms of the diagram
shown below:

Consider the question of coloring the faces of this solid. Since
the dodecahedron has 12 faces, consider the (non-trivial) divisors
of 12: 2, 3, 4, and 6. This means that the faces of the dodecahedron
can be thought of as falling in 2 groups of 6, 3 groups of 4,
4 groups of 3, or 6 groups of 2. Think of all of the faces in
each group as getting the same color. Thus, one can consider coloring
two groups of six faces each with a different color or 3 groups
of 4 faces each with a different color.
Traditional coloring rule:
If two faces have an edge in common, color them with different colors. (If faces meet at a vertex but do not share an edge, they can be colored the same color.)
However, one might consider other coloring rules which might be
of interest. Examples include:
having a coloring where some symmetry (or all of the symmetries) of the polyhedron are "consistent with" the coloring (known as a perfect coloring when all the symmetries are "consistent" with the coloring).
having each color appear at every vertex of the solid (known as a precise coloring).
(Remark: It is possible for a coloring to be perfect but not precise,
precise but not perfect, or both perfect and precise.)
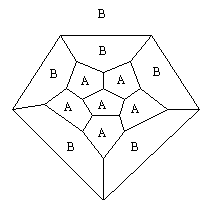
As an example, consider the two-coloring of the dodecahedron with
the colors A and B shown below. This coloring does not obey the
traditional rule for coloring faces nor the rule that each color
should appear at every vertex. However, it has the appealing property
that a "symmetry" of the solid will interchange the
colors. Also, a variety of symmetries will preserve the coloring.
Note that the "infinite" region of the figure must receive
a color and in this case it has been colored "B." (There
are 11 finite faces and 1 one infinite face in this diagram. Pictures
of a similar kind for the other Platonic solids will also have
one "infinite" face.)
Problem
Examine colorings of the Platonic solids as suggested above. (You
might want to start your investigation with the tetrahedron and
work your way up to the more complicated cube and octahedron,
and then the dodecahedron and icosahedron.) Your goal is to enumerate
all of the different possible colorings with a particular number
of colors, subject to some coloring rule.
Extensions:
1. Consider the issue of coloring the vertices of these solids
instead of the faces.
2. Consider the issue of coloring the edges of these solids instead
of the faces.
3. Consider the issue of coloring more than one element at a time, say, the vertices and the faces or the vertices and the edges.
4. When the Platonic solids are constructed with origami paper
of different but solid colors, the result is often striking. Enumerate
the number of different colorings with a particular number of
colors in the origami environment.
5. Extend these ideas to tilings of the plane with regular polygons.
6. Extend to other classes of polyhedra such as the Archimedean
solids and deltahedra (convex solids with all faces equilateral
triangles).
Reference:
1. Ore, O., Graphs and their Uses, Mathematical Association of
America, Washington, 1963. (There is a new revised edition prepared
by R. Wilson.)
A gentle introduction to the theory of graphs which includes a
good treatment of coloring problems and the Platonic solids.
2. Barnette, D., Map Coloring, Polyhedra, and the Four-Color Problem,
Mathematical Association of America, Washington, 1983.
A nice introduction to the theory of polyhedra using the theory
of graphs with special attention to coloring problems.
3. Saaty, T. and P. Kainen, The Four Color Problem, McGraw Hill,
New York, 1977. (Republished by Dover Press.)
A summary of the state of the art for coloring problems right
after the Four Color Theorem was established by K. Appel and W.
Haken.
Previous | Home | Glossary | Next