Definition 1: A net for a polyhedron is a diagonalized plane polygon
which can be folded along the diagonals and assembled into a 3-dimensional
polyhedron.
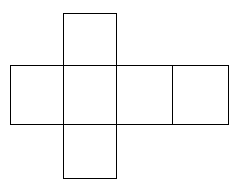
For example, shown below is one of the nets of the cube:
There are, in fact, 10 other non-equivalent nets for the cube!
Definition 2: A deltahedron is a 3-dimensional polyhedron all
of whose faces are equilateral triangles. (Many books reserve
deltahedron for polyhedra which are convex.)
Problems
1. Find the different nets for various convex deltahedra. The
easiest place to start is the tetrahedron. The next "smallest"
example is the solid obtained by pasting two regular tetrahedra
together along a face, and the next simplest after that is the
octahedron. (How does the number of nets of the octahedron which
are non-equivalent compare with the number of non-equivalent nets
for the cube?)
2. Given a plane polygon P which can be triangulated into equilateral
triangles. Can P serve as the net for two non-equivalent polyhedra
all of whose faces are triangles? (See 2. in background section
below.)
3. Given a plane polygon P which can be triangulated into equilateral
triangles. Can P serve as the net for two non-equivalent convex
deltahedra? Can the same triangulated polygon be folded into
a convex and a non-convex deltahedron? Can the same triangulated
polygon be folded into two different non-convex polyhedra?
4. Given a plane polygon P which can be triangulated into equilateral triangles.
Try to produce such a polygon P which can serve as the net of
three non-equivalent polyhedra such that: two of the polyhedra
are convex and the other is non-convex or two are non-convex and
one is convex.
Background:
1. It is still an unsolved problem whether or not every convex
3-dimensional polyhedron has a net. The difficulty is that for
some ways of trying to cut a polyhedron and open it up, the polygons
will overlap when flattened into the plane.
2. Strictly speaking, a net requires pasting instructions as to
which edges are to be pasted to each other, since otherwise there
may be several different polyhedra that can be assembled with
the same net. This fact is explicitly pointed out in the paper
"Polyhedra with convex nets" by G. C. Shephard.
3. Shephard in the paper above raises the question of which polyhedra
have a combinatorially equivalent polyhedron with a net whose
shape is a convex polygon. He gets a variety of results concerning
this question.
Extensions:
1. Investigate other problems which involve nets for polyhedra.
You might consider the case where all the faces of the polyhedron
are rhombuses. (Example: Find all the inequivalent nets for a
solid combinatorially equivalent to a cube but whose faces are
all rhombuses).
References:
1. Beck, A., and M. Bleicher, and D. Crowe, Excursions into Mathematics,
Worth, New York.
2. Pearce, P. and S. Pearce, Polyhedra Primer, Van Nostrand Reinhold,
New York, 1978.
3. Shephard, G., Convex polytopes with convex nets, Math. Proceedings
Cambridge Philosophical Soc., 78 (1975) 389-403.
Previous | Home | Glossary | Next