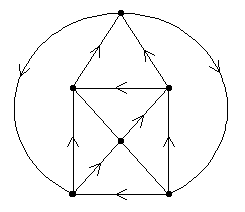
Figure 1
Let G be a k-valent graph (i.e. there are k edges at each vertex).
Problems
1. Can the edges of G be oriented so that for every pair of vertices
v and w of the oriented graph outval(v) = outval (w) and inval(v)
= inval(w)? If not, for what graphs can this be done? (In a directed
graph outval(v) counts the number of edges which are directed
away from vertex v and inval (v) counts the number of edges which
point towards v.) Figure 1, for example, shows for one graph
G, a way of orienting the graph so that at each vertex the invalence
and outvalence are each 2.

2. Repeat this question but in particular for plane graphs (i.e.
graphs which have been drawn in the plane so edges meet only at
vertices). Can the same cyclic pattern be achieved at each vertex
in this case?
Extensions:
1. Are there graphs for which different orientations can be made
which achieve the different possible "identical" patterns
of in and out edges at each vertex? (For example, in a 4-valent
graph one can have all vertices with inval =3 and outval = 1,
or inval =2 and outval = 2, or inval 1 and outval 3 patterns.)
Previous | Home | Glossary | Next