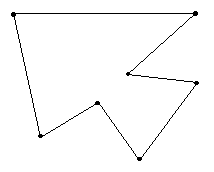
Figure 1
Figure 1 shows a plane polygon with 7 sides.
Figure 1
By adding diagonals, it becomes possible to triangulate the polygon, that is, to have all the regions after the diagonals are added consist of triangles (except for the unbounded region that surrounds the polygon, which will be a triangle only for the case when the original polygon has n = 3 sides).
One way of doing this for the polygon in Figure 1 is shown in
Figure 2.
Figure 2
One can now count the number of line segments that meet at each
vertex of the polygon. The resulting numbers for the triangulated
polygon in Figure 2 are shown in Figure 3.
Figure 3
If the resulting collection of numbers is arranged in decreasing order one obtains what will be called the valence sequence of the triangulated polygon. The valence sequence for the triangulated polygon in Figure 3 is:
Problem
1. Determine those integer sequences which can arise from some
triangulated polygon.
Comment: Triangulated polygons are a special case of a class of
graphs that can be drawn in the plane which are called outerplanar
graphs. These are graphs for which all the vertices of the graph
lie on a single face of the graph.
References:
1. Ore, O., Graphs and their Uses, Mathematical Association of
America, Washington, 1963. (There is a new revised edition prepared
by R. Wilson.)
2. West, D., Graph Theory, Prentice-Hall, Englewood Cliffs, 1996.
Previous | Home | Glossary | Next