Basic Principles of Fairness (8/29/99)
Prepared by:
Joseph Malkevitch
Mathematics and Computing Department
York College (CUNY)
Jamaica, New York 11451-0001
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
Imagine that a circular pie is to be fairly divided by a third party (Nina) on behalf
of Alex and Ben by drawing a diameter through the pie. The pie is 1/4 red, 1/4 white,
and 1/2 green. Unknown to Ben, Alex prefers the white part of the pie and is indifferent between the red and green parts. Alex's preference is indicated by the fact
that in his mind he assigns 80 points as the value of the white part of the pie while
he only assigns the red and green parts a value of 10 points each. Unknown to Alex,
Ben prefers the red part of the pie and is indifferent between the white and green parts.
Ben's preference is indicated by the fact that in his mind he assigns 90 points to
the red region and 5 points to each of the green and white regions. Nina knows the
boys' preferences.
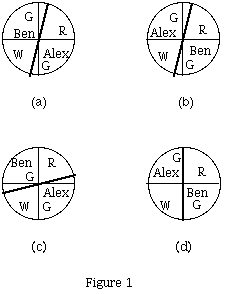
Figure 1 shows four ways Nina could divide the pie and assign pieces to Alex and Ben.
Note that divisions 1 and 2 differ only in who gets which piece. In all four of these
situations each of Alex and Ben get 1/2 of the pie from a physical point of view
but not always 1/2 from the "psychological" view that takes into account the point assignments
to the regions. If there were n people instead of 2, in order to be considered fair
each person would want to receive at least 1/n of the pie with respect to his/her "psychological" point of view. This basic idea in fairness is known as the principle
of proportionality
.
The division in Figure 1 a will make Ben jealous (envious) of the piece that Alex
got and Alex jealous (envious) of the piece that Ben got. Thus, one or more person
may be envious of the piece of pie that another person got, since the person thinks
that the piece that the other person got is better (bigger) than his/her own. Ideally the
division should be envy-free
. In the case of two people proportional solutions are envy-free and conversely. (Can
you prove this?) However, for situations which involve three or more people the concepts
of being envy free and proportional are not equivalent. (Can you think of any examples that show this?)
In light of the fact that Alex prefers the white part of the pie and Ben prefers the
red part, the division in Figure 1 b or c would be superior to the the division in
Figure 1 a. This is because in these solutions each person not only gets what he/she
perceives as half the pie, but, in fact, each person gets what he/she perceives as more
than one half of the pie. This shows that there are division problems where in each
person's mind he/she receives more than an exactly proportional share.
Is the solution found in Figure 1 b or c the best that Nina can find? Clearly not!
As shown in Figure 1 d we have another solution in which each player is happier than
he was with the solution in Figure 1 b or c. In this sense the divisions of the pie
in Figure 1 b or c are inefficient
. In economics the solution in Figure 1 b or c would be said not to be Pareto Optimal
(in honor of the Italian economist Vilfredo Pareto, who was a pioneer in studying
this idea), since there is another solution which makes at least one player happier
and with which the other players are no less happy. This constitutes another fairness
principle, that of efficiency or Pareto Optimality
.
Given the preferences of the boys in this situation, a proportional, envy-free, efficient
solution is possible (Figure 1 d). (In fact, there are other solutions with these
properties. Can you find them?) Unfortunately, there are problems in which these
principles (i.e. proportionality, envy-free, efficient) can not be achieved simultaneously!
Can you find examples for yourself?
References:
1. Balinski, M. and H.P. Young, Fair Representation, Yale U. Press, New Haven, 1982.
2. Brams, S. and A. Taylor, Fair Division, Cambridge U. Press, New York, 1996.
3. Sen, A., Inequality Reexamined, Harvard U. Press, Cambridge, 1992.
4. Young, H.P., Equity, Princeton U. Press, Princeton, 1994.
Acknowledgement
This work was prepared with partial support from the National Science Foundation (Grant
Number: DUE 9555401) to the Long Island Consortium for Interconnected Learning (administered
by SUNY at Stony Brook, Alan Tucker, Director).
Back to list of tidbits
