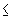k for every pair of vertices u and v in G, then
T is called a k-approximating tree for k.
If G is a connected graph (no loops or multiple edges) then G
has a spanning tree T. (A spanning tree in a graph is a connected
subgraph which includes all the vertices of the graph and is a
tree.)
If u and v are two vertices in G then one can compare the distance
between u and v in G and the distance between u and v using only
edges of the spanning tree T. We will denote the two distances
involved by dG (u,v) and dT (u,v). The distances between two vertices
in the tree is at least as large as the distance between the vertices
in the original graph. When the difference between dG (u,v) and
dT (u,v) is 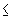k for every pair of vertices u and v in G, then
T is called a k-approximating tree for k.
Problems
1. Study the relationship between the diameter d of G, and the
extent to which dT (u,v) can be used to approximate dG (u,v) closely
(i.e. the value of k within which T approximates G)?
2. Compare how well a spanning tree can be used to approximate
distances in G when G has a unique center, compared with the case
when every vertex of G is in the center.
3. Does a spanning tree in a graph which mininimizes the average
"discrepancy" between tree and graph distances (over
the set of all spanning trees) have any nice properties?
Previous | Home | Glossary | Next