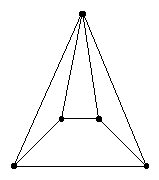
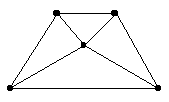
If one draws a plane graph which represents a 3-polytope there
is essentially only one way to do this, even though different
drawings may look rather different. For example, in the Figure
below two different drawings of a 4-gonal pyramid have been drawn.


The number of faces with different numbers of sides for either
of these two drawings is: p3 = 4 and p4 = 1.
(pk denotes the number
of faces with k sides.)
Now consider drawings of a 4-gonal pyramid drawn in a manner so
as to suggest that the 3-dimensionality of the 3-polytope.
An examples of such a drawing is shown below:
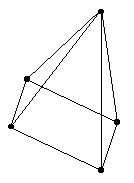
Note that this drawing has extra crossings which do not actually
represent vertices of the drawings. However, suppose that we now
add these "accidental crossings" as additional vertices.
The result for the graph above is shown below:
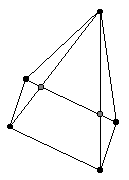
Let us call this procedure making of a graph from a drawing (MGD).
We now get one or more face vectors different from the original
one.
Problem
1. Is there any relation between the set of face vectors that
arise from all the different possible drawings of a fixed 3-polytope
by the procedure described above?
2. For a fixed number of of vertices, which 3-polytope gives
the largest number of face vectors by this procedure?
3. For a fixed number of vertices, which 3-polytope admits some
drawing with the largest number of vertices which have to be added
using the MGD process?
Previous | Home | Glossary | Next