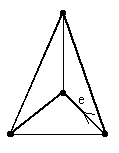
Figure 1
Let G be a plane 3-valent graph and e be one of its edges. Suppose
that by moving along some edge one can generate a circuit which:
a. Closes into a simple closed curve.
b. Passes through each vertex of the graph once and only once
(i.e. Hamiltonian circuit) by following a "coded sequence"
over and over again.
Examples of coded sequences are: L, R, L, R, .... and L, L, R,
R, L, L, R, R, .... where L and R refer to making left and right
turns, respectively, when one gets to the vertex at the end of
an edge.
For example, Figure 1 shows an example of a graph where this occurs
for the the L, R code. The edge e is shown and an arrow indicates
the direction of motion along e. The dark edges are those that
are generated by applying the L, R code.

Problems
1. Determine which 3-valent plane graphs have hamiltonian circuits
generated by the L,R code.
2. Determine which 3-valent plane graphs have hamiltonian circuits
generated by the L,L,R,R code; by the L,R,R,L code.
Extensions
1. Extend your results to graphs which have valence other than
3.
References:
1. Ore, O., Graphs and their Uses, Mathematical Association of
America, Washington, 1963. (There is a new revised edition prepared
by R. Wilson.)
2. West, D., Graph Theory, Prentice-Hall, Englewood Cliffs, 1996.
Previous | Home | Glossary | Next