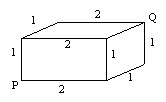
Consider the "brick" which is a rectangular solid which
is 1x1xm where m is an integer. When m =1 we have the cube and
the 1x1x2 brick is illustrated in the figure below. We will think
of the brick as a surface rather than as a solid. When we speak
of the distance between two points on the brick we mean the distance
along (over) the surface of the brick. Points P and Q on an 1x1xm
brick are the points that correspond to the points P and Q labeled
in the figure below:

Problems
1. Determine the possible nets of bricks for different values
of m = 1, 2, ....
(Test your intuition: Do you think there are more nets for m=1
or m=2? m=2 or m=3?)
2. Determine the shortest distance between the points P and Q
as a function of m, the size of the brick.
3. If the point P is fixed, what is the farthest point on the
brick from P? (If there are many points which can be farthest
from P give a description of the set of possible points.)
4. What is the largest distance between any two points on the
the brick? (Can you give a formula for this distance as a function
of m?
Extensions
1. Nothing in the description above requires that m be an integer.
Do any differences in behavior occur for bricks where m is not
an integer?
Previous | Home | Glossary | Next