Everyone is familiar with the ordinary 3-dimensional cube. One
of its features is that it is highly symmetric. In fact, there
are 48 different transformations of the cube that preserve the
cube. (These transformations include rotations, reflections in
lines, and reflections in planes.) In order to understand better
the problem to be posed below we will first consider the analog
of the problem to be considered for the square.
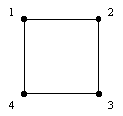
The square shown labeled in the diagram below has 8 symmetries
(isometries) that preserve it. Some of these symmetries are rotations
and some of them are reflections.

These 8 transformations are referred as the symmetry group
of the square. The result of performing one transformation
after another yields another transformation. For example, one
can rotate by 90 degrees followed by a reflection in the line
determined by points 2 and 4.
One way to write down these symmetries is using the notation that
appears below, which tells where each original vertex of the square
is after being transformed. Think of the labels as being fixed
and the points as moving. Record the labels before and after the
motion of the points. Here are the eight transformations, the
top row shows the labels initially and the bottom row the labels
after the transformation is completed:
1234 1234 1234 1234 1234 1234 1234 1234
1234 4123 3412 2341 4321 2143 3214 1432.
This collection of 8 transformations has various subsets of transformations
which are subgroups of the original group. For example, the square
has a collection of 4 symmetries, its rotations, which form a
subgroup of the original group of symmetries. This rotation subgroup
consists of:
1234 1234 1234 1234
1234 4123 3412 2341.
It turns out there are various quadrilaterals which have subgroups
of the symmetry group of the square as their symmetry groups.
For example, the rhombus or the rectangle have four element subgroups
as symmetries. However, no quadrilateral has the rotation subgroup
of symmetries as its exact set of symmetries. It turns out there
are seven types quadrilaterals when looked at from a symmetry
point of view. (Examples: rhombus, rectangle, equilateral trapezoid,
etc.)
Problems
1. A solid which is structurally like a cube will be called a
cuboid. Determine all of the different types of cuboids
from a symmetry point of view. (It will probably be helpful to
make physical models to understand what is going on.)
2. What mixtures of four sided faces can cuboids have? (Are there
cuboids whose faces are all trapezoids and rectangles? All rhombuses
and rectangles? All trapezoids?)
3. For each cuboid consider all the nets of the cuboid that are
possible. How does the number of nets for the cuboid compare with
the number of nets for the cube? (A net of a polyhedron
P is a planar pattern of polygons which can be folded up to form
P.)
References:
1. Budden, F., The Fascination of Groups, Cambridge U. Press,
New York, 1978.
2. Burn, R., Groups: A Path to Geometry, Cambridge U. Press, New
York, 1985.
3. Grossman, I. and W. Magnus, Groups and Their Graphs, Mathematical
Association of America, Washington, 1964.
Previous | Home | Glossary | Next