Joseph Malkevitch
Department of Mathematics and Computer Studies
York College (CUNY)
Jamaica, New York 11451
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
Not so long ago geometry was defined as the branch of mathematics concerned with shape. However, today, geometry would probably be defined as the branch of mathematics concerned with visual phenomena. Whereas symbolic algebra systems such Mathematica and Maple have "automated" many parts of algebra and Calculus, performing complex calculations much more accurately than a human could without the assistance of the software, it is still not possible for a computer vision system to write down a description of a scene that it is viewing! Historically, breakthroughs in mathematics have often come first in geometry and then been made more powerful by "algebratizing" the ideas involved. What follows is an "historical" look at seemingly simple issues involving visual phenomena, culminating in a 25 year-old geometry question that is easy to state and understand, but whose solution is unknown and seems to require new ideas.
An architect wishes to give her client a quick impression of the building she designed for him. We live in a 3-dimensional world but we face the constant need to represent 3-dimensional (3-D) objects in 2-dimensions (2-D). What representation should the architect use?
For simplicity, suppose the building is a rectangular box. Boxes are a special case of a very important class of objects both for lay people and mathematicians, the polyhedral solids. These solids are characterized by being formed from sections of (flat) planes, which are known as the faces of the polyhedron. We see polyhedra all around us in the shapes of buildings, household objects and in nature (e.g. crystals). What is the best way to represent polyhedra, such as boxes, in 2-D?
The architect would probably choose a hidden line parallel projection (parallel lines are shown parallel) view or perspective view. In the latter case parallel lines converge at a vanishing point. Those edges in the back of the polyhedron which would be hidden from view by the rest of the polyhedron are now traditionally shown with dotted lines or thinner lines than the edges of the polyhedron which can be seen.
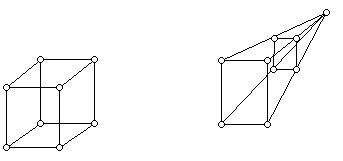
Figure 1 (This diagram shows two ways of drawing a box, one an isometric (parallel lines shown parallel), the other a perspective (parallel lines converge at a single point, hence, look shorter in the distance). Usually, dotted lines show those edges of the polyhedron that are hidden from view by the "front" of the polyhedron.
Such techniques were developed by mathematically inclined artists (e.g. Leonardo di Vinci and Piero della Francesca) during the Renaissance. These artists consolidated ways of constructing 2-D drawings of 3-D objects. Another tool for doing this would be a blueprint, but these diagrams are often hard for lay people to interpret. A more recent tool for representing 3-D in 2-D is that of a graph, a diagram consisting of dots (called vertices) and line segments (called edges). In these diagrams (Figure 2) no attempt is made to capture distance relationships, only combinatorial relationships (which parts are attached to which).
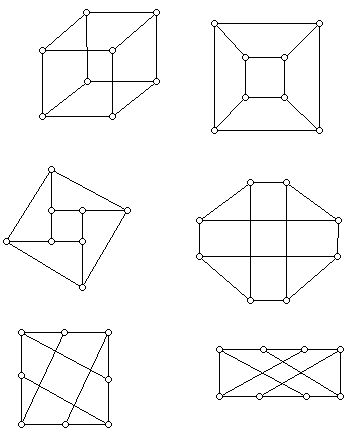
Figure 2 (These diagrams consisting of points and lines (there are 8 dots and 12 line segments) all represent the same structure, though they look very different, namely, a box.
Notice that although all the diagrams in Figure 2 represent boxes, the clearest 2-D representation is in the diagram on the top far right which has been drawn in the plane so that edges only meet at vertices. Graphs may not be useful for an architect's drawings but they have many applications, ranging from chip design to scheduling committees.
Another fundamental way of representing polyhedra in 2-D, the net, is much less well known by the public than the ways mentioned above. The net was also pioneered by a mathematically inclined Renaissance artist, Albrecht Dürer. Figure 3 (on the right) gives the net of the special kind of box we know as the cube, a box all of whose six faces are squares. Starting with a cubical version of a box in Figure 3 (on the left) we can cut along some of the edges (shown darker in the figure) that represent the box (think of the box as a graph for the moment), and by moving the freed panels we can flatten out the squares involved to get the net. To do this one must cut along edges of the cube that include all the vertices of the box but in a way that does not completely cut around any face.
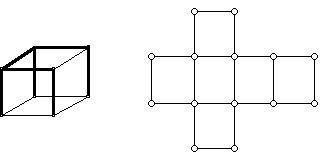
Figure 3 (This diagram shows edges of a cube (on the left) which, when cut and the faces of the cube are unfolded, gives the net of the cube which looks like the letter "t" (on its side).
How many nets do you think a cube has? Would you be surprised to learn that there are 11 different ones, different in the sense that one can not superimpose any of the 11 exactly on top of each other (allowing the pattern to be turned over)?
However, nets are not quite as simple as the diagram in Figure 3 suggests. Strictly speaking, a net requires instructions concerning which edges on the boundary of the polygon that forms the net are to be pasted together. Verify this for yourself by making two copies of the net in Figure 4 and showing that you can paste it together to form either a convex regular octahedron (familiar to many because fluorite crystals have this form) or a non-convex octahedron! (A set is convex if for any pair of points in it, the line segment joining the points is totally within the set.)
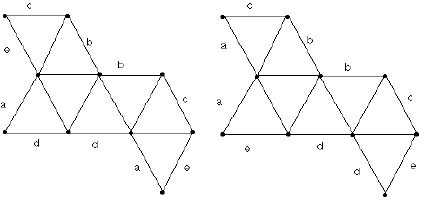
Figure 4 (This diagram shows a collection of 8 equilateral triangles, which when folded together in one way yields the regular octahedron while the same collection when folded a different way yields a non-convex octahedron which, consists of equilateral triangle faces.)
Without the gluing instructions, we do not have enough information to guarantee what polyhedron the net really defines! (One can find examples of polygons (nets) without the gluing instructions that can be folded to form two inequivalent convex polyhedra.)
However, in going from a cubical version of a box on the left in Figure 3 to the net shown there we have glossed over a very fundamental question. It is not difficult to find examples where, for some choice of ways of cutting along the edges of a polyhedron, the faces overlap when we carry out the unfolding! In fact, this can happen for the simplest of convex polyhedra, a triangular pyramid, as shown by an example due to Makato Naniki, which has an overlapping unfolding (see Figure 5, due to K. Fukada), though not all of the unfoldings of the Naniki tetrahedron overlap.
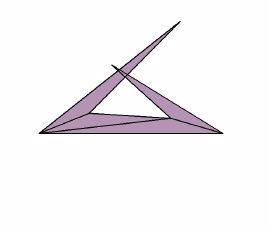
Figure 5 (This diagram shows an attempted unfolding of a tetrahedron where the result is that some of the face panels overlap.)
It was G.C. Shephard, a British mathematician, who in 1975 appears to have been the first to call attention to this simple-to-state but unsolved problem:
Can one always cut along some set of edges of a convex 3-dimensional polyhedron and open the result to form a region in the plane with the property that the panels which form the faces do not overlap?
What is known is that the requirement of convexity is critical, since there are examples of non-convex polyhedra for which no net exists. Thus, any unfolding will overlap for such polyhedra. (Some non-convex polyhedra have unfoldings, but not all of them do.) Other recent research has centered on unfolding a polyhedron by cutting along edge paths that are not exclusively the edges of the polyhedron.
Another remarkable fact is that for "random" convex polyhedra, many of the attempts that one makes to find a collection of cuts that will work to create a net will fail. Thus, if the conjecture is true, it is all the more remarkable, since the set of edges that must be cut to find the proper way to form the net is like finding a needle in a haystack!
It appears that proving Shephard's Conjecture will require new ideas. Though it is unclear whether a resolution of this conjecture has immediate applicability outside of mathematics when new progress is made on subtle problems, invariably it is not only mathematics that benefits but all of society!
References:
Shephard, G.C., Convex polytopes with convex nets. Math. Proc. Camb. Phil. Soc., 1975 (78) 389--403.
Schlickenrieder, Wolfram, Doctoral thesis, 1997.
Additional sources of information on the web are available at La Researche's web page in support of the French version of this article.