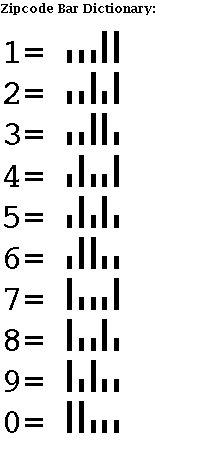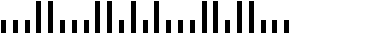Zipcode Bar Code (10/19/2001)
Prepared by:
Joseph Malkevitch
Mathematics and Computing Department
York College (CUNY)
Jamaica, NY 11451
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
Reading the "bars" on your mail
Obtain an envelop which shows the bar pattern used for sorting mail. (Ideally, use
one which has the zipcode of your house (apartment building) on it.) You can do this
by finding an envelop from a bank addressed to your house. A sample is provided below.
Assuming the zipcode uses the ZIP + 4 system it would consist of 52 short and long
bars. This is known as the postnet code and is still commonly used on business reply
forms. (Sometimes only the bars for the original 5-digit zipcode is shown.) However,
starting in 1993, to take advantage of lower rates associated with the use of ZIP + 4,
businesses were required to use a 12-digit bar code known as the deliver-point bar
code. This takes the form of the ZIP + 4 code, followed by the two digits which are
the last two digits of the street address or postal box where the letter is headed. The
bar encoding for this system consists of 62 short and long bars. Thus, if the letter
addressed to your house shows the full 9-digit zipcode and was sent using a meter
system, the bar representation will nearly always have the 62-bar pattern.
Procedure:
Step 1: Erase the initial (first) long bar and terminal (last) long bar, to obtain
a sequence of 60 short and long bars. These extra bars, known as guard bars, are
present to assist the laser which scans the bar code locate the start and end of
the zipcode's bars.
Step 2: Group these 60 bars into groups of 5 bars starting from the left. (One obtains
12 groups of 5 bars.)
Step 3: Decipher each group of 5 bars into the digit it represents using the the table
(deciphering table) below (see page 6).
(What you should obtain is 11 digits. The first 5 of these are the usual zipcode which
codes the municipality that you live in (11530 for Garden City, New York) and the
next four numbers, in the suburbs, represents a code for a specific house (or apartment building or business). In New York City the additional 4 digits may represent a building
or even a floor of a building. Finally, the last two of the 11 digits should be the
last two digits of your street address (or that of the apartment building you live in or postal box that you use).
Puzzle:
Can you figure out how the 12th digit you obtain was chosen? (Remember that your zipcode
only uses 11 digits which can be coded using 55 bars.) For what purpose do you think
this last digit is present? (Note if you are using an envelop where there are only 50 bars after the guard bars are removed, can you figure out how the 10th digit you
obtain was chosen?)
Hint:
Step 4: Assuming you started with a 60-bar code (after the guard bars were removed), add up the 11 digits that have been decoded and add on the last digit.
Do you notice any pattern? (In order to guess the pattern you might have to try several different 60-bar code patterns. All mail that comes to your home will have the
same pattern so you need to try a code obtained from a relative or friend!) Note:
The same system is used in arriving at the 12th digit for a 60-bar code as is used
to get the 10th digit for a 50-bar code.
Note: The solution to the puzzle is given at towards the end!
Warning:
In mail addressed to private homes the bar code imprinted by the post office on the
envelop nearly always corresponds to the actual zipcode digits that are shown. However,
on some business reply envelops the bar code pattern sometimes does not actually
code the zipcode digits shown. This seems to be done by the companies involved to help
distinguish between mail which which is being paid for by the company and mail which
is being paid for by the sender.
Zipcode Bar Dictionary:
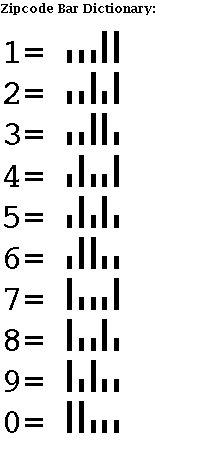
Figure 1
Example (no check digit included):
11530 =
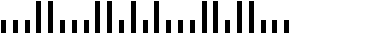
Figure 2
Note:
The counting system that we ordinarily use is called decimal
because it uses ten symbols for digits (e.g. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) together
with place notation (e.g. 12 is different from 21). In the decimal the number one
hundred twenty is represented: 120. Using the decimal system we can represent arbitrarily large numbers. The same, however, can be said of the place notation system called
binary
, which uses only two symbols. When one counts in binary the way one counts from zero
to 9 is: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001. In binary the number 120 is represented: 1111000
If one "pads" the representations of the digits from 0 to 9 on the left to result
in 5 digits one obtains: 00000, 00001, 00010, 00011, 00100, 00101, 00110, 00111,
01000, 01001. Note that these are not the 5-digit binary sequences used to represent 0-9
above. The reason for this is to note that what is given above is not the counting sequence representation
for the numbers from 0 to 9 but a code for the numbers from 0 to 9. This code has
binary sequences of five digits exactly two of which are ones. You can check that there are exactly 10 of these. The numbers are assigned, lexicographically, that
is, as if one were constructing a dictionary for them where 0 is considered to come
before 1.
Back to list of tidbits