Geometrical Skeletons Tidbit (9/11/02)
prepared by:
Joseph Malkevitch
Department of Mathematics and Computer Science
York College (CUNY)
Jamaica, NY 11452
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
Suppose one is trying to design a program to recognize the shape of printed letters. Think of each letter as being two-dimensional, that is the letters are fat. For example, the diagram below shows the letter F.
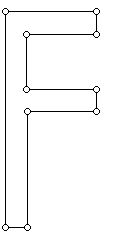
One can imagine that the shape of this 2-dimensional letter is thinned down to obtain a one-dimensional representation of the F. The original F with a thinned representation of the F is shown in the next diagram:
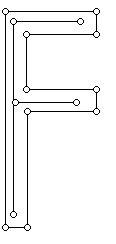
This idea suggests the value of being able to take a 2-dimensional shape (for simplicity, think of it as a plane simple polygon, which is either convex or non-convex) and being able to associate with the polygon something 1-dimensional which captures the essence of the shape of the original. This approach was pioneered in a appear by H. Blum in 1967, when he introduced the idea that today is referred to as the medial axis of a polygon. (The thinning above is not the medial axis of the letter F. )
Before introducing a definition of the medial axis let us first review some basic facts from Euclidean Geometry. In our discussion below we assume that we are working with the Euclidean distance function, but similar questions and issues come up for other distance functions in 2-dimensions, say, the taxicab distance.
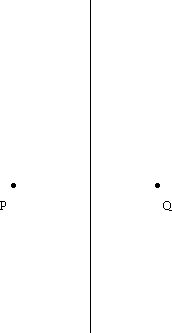
Given two points, what is the set of points equidistant from them?
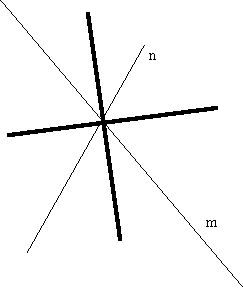
Given two lines, what is the set of points equidistant from them?
Given a point and a line, what is the set of points equidistant from them?
The points which are equidistant between two fixed points lie on a line which is perpendicular (right angles) to the line which joins the two points and passes through the midpoint of the segment that joins them.
To understand the situation of finding points which are equidistant from two lines we have to consider two cases:
a. The lines are parallel
In this case the collection of points equidistant from the lines is another line which is parallel to the original two and which is half the distance between them.
b. The lines intersect
In this case the collection of points equidistant from the two lines is a pair of perpendicular lines which bisect the angles at the point where the two original lines meet.
The solution of the two problems raised above involves lines, which can be described using first degree equations. The situation with finding those points which are equidistant between a point and a line is the most complex. The answer is that the set of points involved lie not on any line but on a curve, called a parabola, which has a second degree equation.
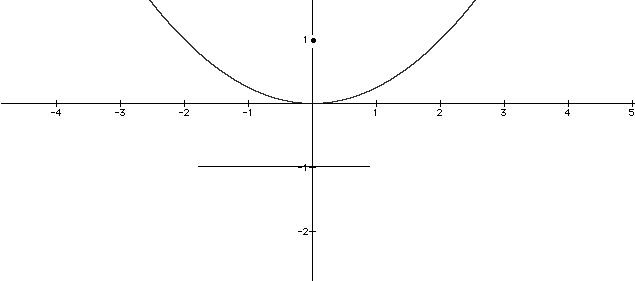
The parabolic curve shown is the set of points equidistant from the point (0, 1) and the line y = -1, a portion of which is shown in the diagram above. Its equation is y = x2/4.
We are now prepared to look at the problem of computing the medial axis of of some simple geometric objects. We will confine our attention to plane polygons and will make use the following definition:
If P is a plane polygon, the medial axis of P will be the set of points within P with the property that they have more than one closest point along the boundary of P.
The diagram below illustrates the medial axis for a (non-square) rectangle:
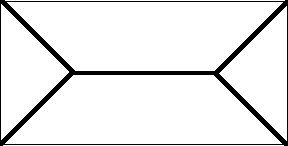
For clarity of visualization, the medial axis is shown in bold black lines and the original polygon in thinner black lines. As a graph theory structure the medial axis is a tree structure (i.e. a connected graph which has no circuits). The vertices having valence 3 in this tree indicate that at these points there are three locations on the boundary of the original polygon which are closest to these vertices. (Can you figure out where these three points are? None of them are corners of the original rectangle.) The medial axis for a square would have been the tree structure consisting of the diagonals of the square. As a tree, this graph would have one 4-valent vertex.
You should try to some experiments to help you understand how the medial axis behaves.
For example:
What is the medial axis of a triangle?
Answer: The medial axis consists of pieces of the angle bisectors of the three angles of the triangle, as shown in the diagram below:
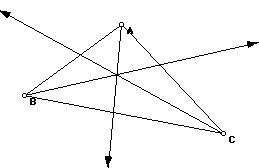
Can you figure out what portions of the angle bisectors to remove in order to have only the medial axis remain?
It is interesting to see what happens to the structure of the medial axis of a triangle, when one cuts off the corner of one of the vertices of the triangle to get a quadrilateral.
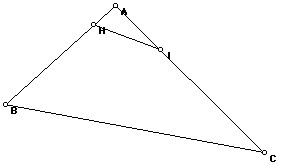
In the diagram shown the original triangle is ABC and the vertex A has been cut off to form the quadrilateral BHIC. What is the medial axis for this polygon?
You may be interested in the following rather nice theorem in helping you understand what is going on.
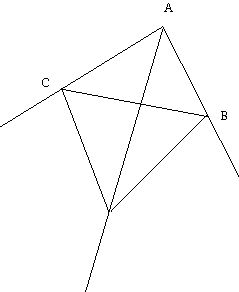
In the triangle ABC above, the external angles of the triangle at B and C have been drawn. Remarkably, the point where these external bisectors meet is concurrent (i.e. passes through a common point) with the angle bisector through A.
Can you use this theorem to figure out what the medial axis for the quadrilateral BHIC is?
If you try a few experiments using convex polygons you will be able to verify that the structure you get as the medial axis is always a tree consisting of straight line pieces. What happens if the polygon is non-convex? It turns out that the result does not always consist of straight line segments even though the medial axis will be a tree structure in graph theory terms. Can you see why, using the ideas above, the curved segments which may occur in the medial axis for some non-convex polygons consist of pieces of parabolas? To practice your understanding of these ideas you can try constructing the medial axis for the fat F at the very start of our discussion. One might consider it a flaw of the medial axis concept that it does not consist of a tree structure of straight line pieces. Researchers have found other ways to define the skeleton of a plane simple polygon that have the nice feature that the resulting skeleton consists of straight line sections which form a tree.
Although there is a large literature on the medial axis, here are some research problems that I have not seen explicitly answered in the literature which discusses the medial axis.
Problem 1:
When a parabolic piece of the medial axis meets a linear piece at a point where exactly two pieces of the medial axis adjoin, what angles can the pieces meet at?
Problem 2:
Under what conditions (if any) will the medial axis of a non-convex polygon consist of only straight line segments?
Problem 3:
Let P be a convex polygon with n sides. What are the set of face vectors of the faces formed by the medial axis with the original polygon (treating the n-gon of the original P as the infinite face)? (For example, for the non-square rectangle above, the medial axis divides the plane into 5 regions, two triangles, and three 4-gons.)
Problem 4:
Develop intuitively appealing ways to compute the medial axis for a convex polygon. (The optimal complexity for this problem is known.)
Problem 5:
Given a plane tree which does not intersect itself, when is there a plane simple polygon whose medial axis is the given tree?
References:
Aichholzer, O., and F. Aurenhammer, D. Alberts, and B. Gärtner. A novel type of skeleton for polygons, J. Universal Computer Science, 12 (1995) 752-761.
Aichholzer, O., and F. Aurenhammer. Straight skeletons for general polygonal figures in the plane, Proc. 2nd Annual International Conference Computing and Combinatorics, pp. 117-126. Lecture Notes in Computer Science 1090, Springer, 1996.
Blum, H., A transformation for extracting new descriptors of shape, in W. Wathen-Dunn, (ed.), Models for the Perception of Speech and Visual Form, MIT Press, Cambridge, 1967, p. 362-380.
Chin, F., and J. Snoeyink, C. Wang, Finding the medial axis of a simple polygon in linear time, Proc. 6th Ann. Int. Symposium Alg. and Computation (ISAAC 95), Lecture Notes in Computer Science, 1004, Springer-Verlag, 1995, 383-391.
Kirkpatrick, D., Efficient calculation of continuous skeletons, Proc. 20th. Annual IEEE Symp. on Foundations of Computer Science, 1979, 18-27.
Klein, R. and A. Lingas, Fast Skeleton Construction, Algorithms---ESA '95, Third Annual European Symposium, Lecture Notes in Computer Science, Vol. 979, 1995. pp. 582-595.
Lee, D., Medial axis transformation of a planar shape, IEEE Trans. on Pattern Analysis and Machine Intelligence, 4 (1982) 363-369.
Back to list of tidbits








