An Elegant Proof of the Pythagorean Theorem (10/04/2002)
Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
web page: www.york.cuny.edu/~malk
Here is a derivation of the Pythagorean Theorem, based on an argument due to President James Garfield.
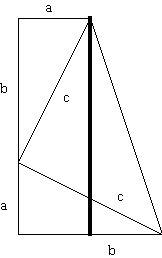
The proof makes use of an area argument, which starts by observing the special trapezoid in the diagram below:

Recall that the area of a rectangle is the product of its length times its width, and that the area of a right triangle is given by the the product of its legs divided by 2.
The area of the trapezoid can be computed in two different ways. First, one can write the area as the sum of the areas of the rectangle and triangle that share the bold line in the figure.
Based on this we have that the trapezoid's area is:
(a + b)(a) + (a + b)(b-a)/2.
Simplifying this expression we have that: a2/2 + ab + b2/2 is the area of the trapezoid.
However, the area of the trapezoid can also be computed as the sum of the areas of three triangles. Two of these triangles are congruent to each other, and have the same area so we have the area of the trapezoid is given by:
ab + c2/2.
Setting our two expressions for the area equal to each other we get:
ab + c2/2 = a2/2 + ab + b2/2
Simplifying we obtain: a2 + b2 = c2.
Thus, we have verified for a right triangle with sides a, b, and c we have:
a2 + b2 = c2.
Of course, the Pythagorean Theorem does not hold in Bolyai-Lobachevsky Geometry (also known as Hyperbolic Geometry). Thus, the proof must somehow depend on the parallel postulate of Euclid. Do you see where in the proof we used the parallel postulate?
Reference:
Loomis, E.S., The Pythagorean Proposition, National Council of Teachers of Mathematics, 1968.