Figure 1
The Mathematical Legacy of Victor Klee
Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/
Victor Klee was one of America's most prominent geometers. His recent death (August, 2007) is a great loss for the mathematics community. HIs published works included several books and over 240 research papers. Klee was born in San Francisco in 1925 and attended Pomona College with a major in both mathematics and chemistry. He received his doctorate degree from the University of Virginia where he studied with the prominent topologist Edward McShane. HIs doctoral thesis (1949) was entitled:
Convex Sets in Linear Spaces
Most of Klee's career was spent at the University of Washington (Seattle) where he joined the faculty in 1953 and retired from that university in 2000. In his years at the University of Washington, Klee supervised 34 doctoral students. His students in turn have trained many additional geometers. According to the Mathematics Genealogy Project, Klee has 100 mathematical descendants (and he had "regular" children and grandchildren as well). From 1971-1972 Klee served as the president of the Mathematical Association of America. Klee's contributed to combinatorics, convexity, algorithms, and optimization problems but his work always had a strongly geometric flavor.
Klee's Mathematics
Klee's mathematics ranged across many aspects of geometry. He made especially important contributions to the theory of convex polytopes, notably, polytopes in higher dimensional spaces. A polytope is a bounded convex set which is the intersection of the higher dimensional analogue of planes. (Note: A set is convex when for any two points p and q in the set, the line segment joining p and q is also in the set.)
I would like to call attention to three important results that Klee was involved with which can be discussed in elementary terms: Art Gallery Theorems, the Klee-Minty Polytopes, and Kleetopes.
Of these three, the role Klee played in the development of "art gallery" theorems is the most recent. In 1973 the young Czech mathematician Vasek Chvatál challenged Victor Klee to describe an "interesting" problem in elementary geometry. Klee responded with the following problem.
Suppose we are given a plane simple polygon with n sides. The polygon can be thought of as the floor plan of a bank, museum, or art gallery. We desire to put sensors at some of the vertices of the polygon so that collectively these sensors can see or guard all of the points in the interior of the museum. A point p in the interior of the polygon is said to be visible from a vertex v of the polygon if the line segment pv contains no points from the exterior of the polygon. (This condition is not very realistic. It means that a point p can be visible from a vertex v even if the line from v to p includes many isolated vertices or even segments from the boundary of the polygon. However, it is mathematically convenient to describe the problem this way.)
Although Klee had a conjecture that there were some n-gons that required floor function of n/3 vertex guards, and that there are no n-gons which ever require more than floor function of n/3 guards, he could not prove this. Chvatál gave the first proof of this conjecture, but it was Steve Fisk who provided a truly elegant way to see what was going on.
A common misunderstanding of this problem is that what is being asked for is an algorithm which finds for a given fixed polygon P what is the minimum number of vertex guards for the polygon P. This is clearly both an interesting an important problem, however, unfortunately, all known algorithms for this problem require an exponential amount of work as a function of n, the number of sides of the polygon. More precisely, it is known that this problem is NP-Complete. This means, that it is unlikely that there is a polynomial time algorithm which finds the minimum number of guards for a fixed polygon P.
Early on in the history of polyhedra, the question of whether or not a polyhedron had a simple closed circuit which included all its vertices, a hamiltonian circuit, has been of interest. Part of this interest stemmed from the fact that if a 3-valent convex polyhedron has a hamiltonian circuit then its faces can be colored with 4 colors. (It turns out that this approach to the 4 color problem will not work since there exist non-hamiltonian 3-valent polyhedra, the first such example being due to W.T. Tutte.) It was natural that Klee would have an interest in whether high dimensional polyhedra always had hamiltonian circuits. This was in part because of his keen interest in linear programming problems, and theoretical questions associated with paths on polytopes. Using a very simple idea Klee showed that there existed non-hamiltonian polytopes in every dimension.
His idea can be illustrated in three dimensions using the idea that has come to be called a Kleetope.
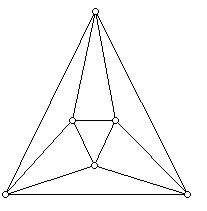
One starts with a polyhedron all of whose faces are triangles. An example of a graph of such a polyhedron is shown in Figure 1

The graph is the graph of the regular octahedron. Note that it has 6 vertices and 8 faces. What Klee does to construct a non-hamiltonian polyhedron is to erect a pyramid on every face of this polyhedron. The construction is carried out in Figure 2.
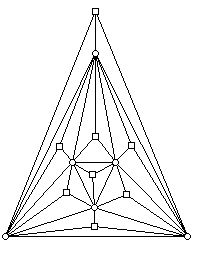
The original vertices from Figure 1 are shown with circles and the new vertices, which are the "apexes" of the pyramids are shown as squares. Note that this graph is not a bipartite graph. Square vertices are only joined to circle labeled vertices but circle labeled vertices are joined to both circle labeled vertices and square labeled vertices. The graph above can not have a hamiltonian circuit since to get to a square vertex one must have come from a circle vertex but there are not enough such vertices to form a simple circuit with the square vertices. The diagram above is a combinatorial diagram, and for this graph, Steinitz's Theorem guarantees the graph can be realized by a convex 3-dimensional polyhedron. However, one does not have to invoke Steinitz's Theorem for this purpose, as Klee observed. Suppose one picks a particular triangle of the polyhedron in Figure 1. If one selects a point very close to the plane that forms this face, above the interior of this face, then a "flat" pyramid over this face will not destroy the convexity of the resulting new polyhedron. This process can be carried out for each of the faces of the original polyhedron in Figure 1 in turn until one gets a polyhedron with the same graph as the one in Figure 2.
The analogous idea can be carried out in d dimensions, where no analogue of Steinitz's Theorem is known to hold.
Finally, let me make some comments about the Klee-Minty Polyhedra. This work was joint with George Minty. Many of Klee's papers grew out of an interest that he had in linear programming problems. Linear programming is a discrete optimization model where the goal is to maximize or minimize a linear expression where the the values that occur in the linear expression lie within a convex polyhedron. Linear programming problems arise in a wide variety of fields including resource allocation, scheduling, and blending. Very large numbers of these problems are routinely solved every day by American businesses and governments. George Dantzig was responsible for developing a very attractive algorithm for solving linear programming problems which seemed to work extremely well on very large problems. However, he was unable to show a theoretical basis for guaranteeing the the algorithm was efficient for solving very large linear programming problems. What Klee and Minty did was construct a family of polyhedra which had an exponentially growing number of vertices as a function of the dimension and for which when one applied the the simplex method for solving an LP problem on these polyhedra that the method required that one visit all of the polyhedron's vertices before reaching the optimal value. This family examples showed that the simplex algorithm could require an exponential amount of work. For reasons that are not totally clear, examples of real world linear programming problems do not display this kind of behavior. In practice, very large linear programming problems are typically solved very quickly using the simplex method.
References:
Chvátal, V., A combinatorial theorem in plane geometry, JCT (B), 18 (1975) 39-41.
Fisk, S., A short proof of Chvátal's watchman theorem, JCT (B) 24 (1978) 374.
Grünbaum, B., Convex Polytopes, Wily, New York, 1967.
Honsberger, R., Mathematical Gems II, Mathematical Association of America, Washington, 1976, p. 104-110.
Klee, V. and G. J. Minty. How good is the simplex algorithm? In O. Sisha, editor, Inequalities III, pages 159--175. Academic Press, 1972 Meisters, G., Polygons have ears, Amer. Math. Monthly 82 (1975) 648-651.
O'Rourke, J., Art Gallery Theorems and Algorithms, Oxford U. Press, New York, 1987.