Block Design Tidbit (12/14/2004)
prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, NY 11451-0001
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
The theory of block designs (and the theory of more general structures called designs that it spawned) evolved from a variety of sources. On the one hand concepts related to block designs had roots in statistics. The idea was to develop combinatorial structures which would help statisticians determine if, for example, certain identical plants responded better or worse to different fertilizers or other differences in the the way they were grown. Since each plant was growing in a slightly different place in what was hopefully a uniform field, the goal was to try to make sure that any differences that were observed in the plants was due to the different fertilizers rather than mere random variations.
Another source of interest in block designs was to try to extend geometric ideas from the infinite geometries of Euclid, the sphere (real projective geometry), and Bolyai and Lobachevsky to finite analogs of these geometries. Thus, there was interest in constructing finite affine (Euclidean geometries), finite projective geoemtries, and finite Bolyai-Lobachevsky geometries.
What are block designs or, as they are more commonly known, BIBDs (Balanced Incomplete Block Design)?
We start with a set of objects variously referred to as points or varieties (showing the statistical origins of the idea) denoted by V, as well as a collection B of subsets of V, called blocks (or lines), all of which have the same number of elements k. We insist that every element of V be contained in exactly r blocks and that any pair of elements of V lie in exactly λ blocks. The number of elements in V, v, and the number elements in B, b, as well as k, r, and λ are called the parameters of the block design.
These parameters must satisfy the following obvious conditions:
vr = bk
r(k - 1) = λ (v - 1)
Parameters that satisfy these equations are called admissible.
Note that if one is given v, k and λ then the remaining two parameters are determined as: r = λ(v - 1)//(k - 1) and b = vr/k.
One early result on block designs was proven by the British statistician and mathematician R. A. Fisher, and is often referred to as Fisher's inequality. Fisher showed that for a block design where 2 ≤ k < v then b ≥ v.
Here are some very simple examples of BIBDs that illustrate the roots of interest in this subject within geometry.
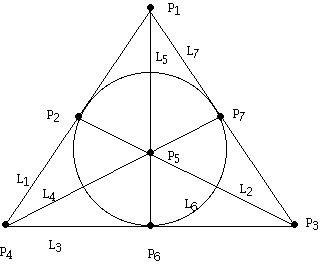
Consider first the diagram which can be interpreted as a BIBD:

Think of the dark dots as elements of V (which I will call points), so v = 7. In addition there are 7 blocks (which I will call lines), which are represented by the 3 sides of the triangle, the 3 cevians, and 1 block, which physically looks like a circle. This finite geometry has 3 points on every line (k = 3) and 3 lines passing through every point (r = 3), and every pair of points lies on exactly one line ( λ = 1). Note that every pair of lines intersect in exactly one point, that is, have exactly one point in common. Thus, this structure has a claim to be thought of as a projective plane, because there are no parallel lines! This particular finite projective plane is known as the Fano Plane, in honor of Gino Fano, the Italian mathematician who was an early pioneer in the study of finite plane geometries and finite spaces.
Now consider the following diagram which also can be interpreted as a BIBD:
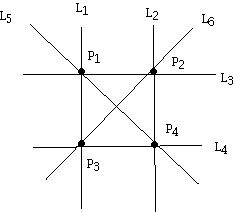
This diagram can be thought of as having 4 points (v = 4), 6 blocks or lines, and k = 2 (2 points on every line), r = 3 (3 lines through every point) and again, every pair of points lies on exactly one block ( λ = 1). Note that unlike in the diagram above where every pair of lines met in exactly one point, here, some of the lines meet and others are parallel. In fact, the lines break up into 3 groups of 2 lines each, where within the groups the lines are parallel but any two lines from different groups will intersect. These groups of lines, where the lines in each group have no point in common are called parallel classes.
It turns out that every finite affine plane can be completed to a finite projective plane by adding one new line (at infinity) to the old plane. The points of this new plane are all of the old points together with the points on the new line at infinity. This line has one new point for each parallel class in the affine plane. Think of each new point on the line at infinity as being where the lines in a single parallel class of the affine plane would meet "at infinity." This adds one new point to each pre-existing line. Also, by omitting one line (and the points on it) from a finite projective plane one gets a finite affine plane.
For finite affine planes it is traditional to say they have order n if they have n points on a line, in which case the parameters of the plane asa BIBD are: (v, b, r, k, λ) = (n2, n2 + n, n + 1, n, 1).
For finite projective planes it is traditional to say they have order n if they have n + 1 points on each line. (The reason being the classical construction described above which adds one point to each line of a finite affine plane.) The parameters of this as a BIBD are (n2 + n + 1, n2 + n + 1, n +1, n + 1, 1). The symmetry of these numbers is a reflection of the fact that there is a duality (interchangeability) between the points and lines of a finite projective plane.
It has been shown that for every n equal to the power of a prime there is a finite affine plane of order n and a finite projective plane of order n. It is also known (using computers) that there is no finite projective plane of order 10. The other other facts known are that infinitely many values of n as orders of finite affine or projective planes are ruled out by a theorem of R. H. Bruck and H. Ryser. It is a major open problem in the theory of block designs (combinatorics) whether or not the only orders for finite affine and projective planes are the prime powers.
When a block design has the property that one can partition the set of blocks into classes, known as parallel classes, each of which partitions the set V of points, then the block design is called resolvable. An obvious necessary condition for the existence of a resolvable BIBD is that k divides v. Another, condition which is not obvious, is the b ≥ v + r - 1.
In addition to applications in statistics, block designs have found a variety of other applications. In particular, ideas concern block designs (and their relatives) have been used to solve scheduling problems in sports (chess, bridge, whist, baseball, etc.) and other situations.
References
Abel, R. and W. Mills, Some New BIBDs with k = 6 and λ =1, J. Combin. Des., 3 (1995) 381-391.
Beth, T. and D. Jungnickel, H. Lenz, Design Theory, Cambridge U. Press, London, 1986.
Bruck, R. and H. Ryser, The non-existence of certain finite projective planes, Canadian J. Math., 1 (1949) 88-93.
Colbourn, C. and J. Dinitz, (eds.), The CRC Handbook of Combinatorial Designs, CRC Press, New York, 19996.
Dembowski, P., Finite Geometries, Springer-Verlag, New York, 1968.
Dinitz, J. and D. Stinson, (eds.), Contemporary Design Theory: A Collection of Surveys, Wiley, New York, 1992.
DiPaola, J. and J. Wallis, W. Wallis, A list of (v, b, r, k, λ) designs for r ≤ 30, Cong. Numer., 8 (1973) 249-258.
Hanani, H., On resolvable balanced incomplete block designs, J. Comb. Theory A17 (1974) 275-289.
Hanani, H., BIBDs with block size 7, Discrete Math., 77 (1989) 89-96.
Lindner, C. and C. Rodger, Design Theory, CRC Press, New York, 1997.
Sadovskii, L. and A. Sadovskii, Mathematics and Sports, American Mathematical Society, Providence, 1993.