Mathematics 243 (Combinatorial and Discrete Geometry)
Review: Examination I
prepared by:
Joseph Malkevitch
Mathematics Department
York College (CUNY)
Jamaica, NY 11451
email: joeyc@cunyvm.cuny.edu
web page: http://www.york.cuny.edu/~malk
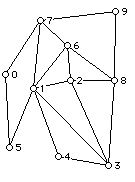
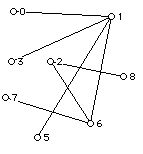
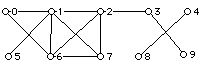
1. For each of the three graphs below:
G:

H:
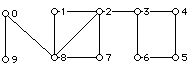
H:
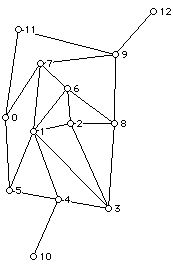
a. Find the number of vertices and edges of the graph.
b. Write down the valence sequence of the graph.
c. Determine if the graph is connected and the number of components in the graph.
d. Write down (if possible) a walk from 2 to 2 that is not a trail.
e. Write down (if possible) a trail from 3 to 5 which is not a path.
f. Write down all the paths from 3 to 6.
g. Determine the cut vertices of the graph, and for any cut vertices that there are the number of components if the cut vertex is removed.
h. Determine the bridges (cut edges) of the graph, and for any bridge that the graph has the number of components if the bridge is removed.
i. Draw the graph with the vertex 5 removed.
j. Draw the graph with the vertex 4 removed.
k. Draw the graph with edge (1,2) removed.
l. If the graph has an Eulerian circuit write one down (using both Fleury's method and showing the use of the wander at random rule with at least one interpolation), and if there is no Eulerian circuit give a reason why.
m. If the graph has an open Eulerian trail write one down, and if there is none give a reason why.
n. Solve the Chinese postman problem for the graph. As part of your solution include the associated closed walk.
o. If the graph has a Hamiltonian cycle write one down. If the graph has no Hamiltonian cycle can you give an explanation of why not?
p. If the graph has a Hamiltonian path write one down.
q. Does the graph have two vertices which are not the end vertices of a Hamiltonian path? (If so, what are they.)
r. Does the graph have two vertices which are not the end vertices of an open Eulerian trail? If so write such a pair of vertices down.
s. Write down a cycle of length 3, if there is one.
t. Write down the longest cycle in the graph.
u. Write down a circuit which is not a cycle if one exists.
v. Is the graph Hamiltonian connected?
2. Draw, if possible, a connected graph, disconnected graph, multigraph, and pseudograph with the valence sequences below. Show drawings when possible which have and lack multiple edges and loops.
a. 2, 2, 2, 2, 2, 2, 2
b. 5, 5, 3, 3, 2, 2, 2, 2, 1, 1
c. 5, 3, 2, 2
d. 6, 4, 4, 4, 3, 3, 2, 2, 2
e. 7, 5, 4, 4, 4, 3, 2, 2, 2, 2, 2
3.
a. If possible draw at least two non-isomorphic graphs whose degree sequence is:
6, 4, 3, 3, 3, 3, 2, 2, 2
b. Draw two graphs which have the same degree sequence and both have 10 vertices and 14 edges but are not isomorphic.
c. Can a graph have 17 3-valent vertices and vertices of no other valences?
4. Can you redraw the graphs below in the plane without "accidental crossings?" What is the number of crossings of the original drawing and one with a minimal number of crossings? What is the crossing number of each of these graphs? Are any of these graphs bipartite?
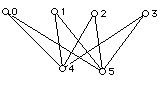
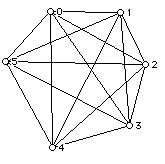
5. Draw graphs with the following properties, if possible:
a. 9 vertices, 5 edges.
b. connected multigraph with 7 vertices and 12 edges.
c. bipartite, 8 edges, connected.
d. A graph with 6 bridges.
e. A graph with 5 cut vertices.
f. A graph which has an Eulerian circuit but no Hamiltonian cycle.
g. A graph which has an Eulerian circuit and has a Hamiltonian cycle.
h. A graph which has no Eulerian circuit and no Hamiltonian cycle.
i. A graph which has no Eulerian circuit but has a Hamiltonian cycle.
j. A graph which has an Eulerian circuit but no Hamiltonian path.
k. A graph which has an Eulerian circuit and has a Hamiltonian path.
l. A graph with 4 odd-valent vertices but for which the best solution of the Chinese postman for this graph requires 10 repeated edges.
m. A graph with an Eulerian circuit where some vertex other than the start vertex must be revisited exactly 5 times.
n. Draw a graph with no 1-valent vertices and no cut vertices that has no Hamiltonian cycle.
o. Draw a 4-valent bipartite graph.
6. Prove that if G is connected and has an Eulerian circuit it must be even-valent.
7. Prove that if G is connected and only has an open Eulerian trail from u to v then only vertices u and v of G are odd-valent.
8. Prove that if G is bipartite and has a Hamiltonian circuit that G must equal numbers of two types of vertices called "circle" and "square."
9. Draw the complete graphs with 4, 5, and 6 vertices.
10. Use the nearest-neighbor heuristic and sorted edges heuristic to find a TSP tour in the graphs below. (When you apply NN use the heuristic first from vertex 3 and then from vertex 1. Do you get the same answer in each case? Do either of these heuristics yield an optimal answer? Do the weights in these graphs obey the triangle inequality?
G:
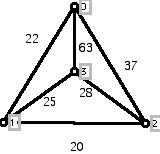
H:
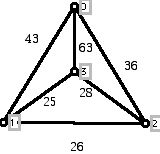
11. Consider the weighted graph below:
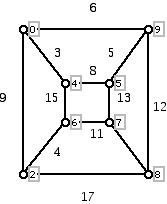
a. Write down a path from 6 to 9. How many edges are in your path? What is the weight of this path? What is the distance between 6 and 9? (Remember that the distance between two vertices is minimum weight sum on any path between the two vertices?
b. What is the largest number of edges that any path from 6 to 9 can have? What is the sum of the weights along the edges of this path? Is the path you found the longest possible path with this largest number of edges?
12. Give "real world examples" where one would have to solve the Chinese Postman problem.
13. Give "real world examples" where one would have to solve a Traveling Salesman problem.