
Research Resources for High School Students Related to Art Gallery Theorems
Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
web page: http://www.york.cuny.edu/~malk
Klee-Chvatal-Fisk Theorem
Given a plane simple polygon P with n sides, how many vertex guards are sometimes necessary and always sufficient to guarantee that every interior point is visible by one (or more) of the guards? (A point v on the boundary of P sees point w in the interior of P if the line segment from v to w contains no points in the exterior of P. This means that a line of sight starting at a boundary point passing through vertices or sides of the polygon on the way to an interior point is permitted.)

The answer to this question, first asked by the American geometer Victor Klee (now retired from the University of Washington), was conjectured by him to be ⌊n/3⌋ where ⌊x⌋ denotes the floor function of x. (This function for a given real number computes the largest integer which is less than or equal to x.) A few years after Klee posed this question Vasek Chvatal provided a proof that Klee's conjecture was correct. Several years after that, a very elegant proof was given by Steve Fisk (Bowdoin College). Fisk's proof used graph theory ideas, specifically, coloring the vertices of a triangulation of the original polygon using the existing vertices of the polygon.) Sometimes the circle of ideas related to this theorem are known as Art Gallery Problems.
There are many specialized kinds of polygons that one might look at with regard to art gallery problems. One particularly interesting class of such polygons is known as rectilinear or orthogonal polygons. A typical example appears below:
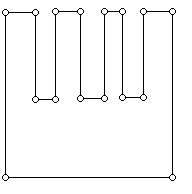
All the angles in this polygon are either 90 degrees or 270 degrees. Can you discover for yourself a conjecture about the number of vertex guards that are sometimes necessary and always sufficient to see the interior of such a polygon?
Some books and web sites to purse this area, which is actively researched but still teeming with unsolved problems, follows.
Books:
O'Rourke, Joseph, Art Gallery Theorems and Algorithms, Oxford U. Press, Oxford, 1987.
This book put art gallery theorems on the map, and though it is "out dated" in the sense that so much has been discovered since, it is still is very useful to look at. The exposition is extraordinarily clear and the material ranges over a wide array of topics that support work on art gallery problem.
Survey articles:
Urrutia, Jorge, Art gallery and illumination problems, in Handbook of Computational Geometry, J.-R. Sack and J. Urrutia, editors, North-Holland, Amsterdam, 2000.
O'Rourke, Joseph, Visibility, in Handbook of Discrete and Computational Geometry, Second Edition, Jacob E. Goodman and Joseph O'Rourke, editors, Chapman & Hall/CRC, Boca Raton, 2004.
Open problems and generalizations
A few questions related to art gallery theorems that I would like to see investigated follow.
1. A polygon is equilateral if all of its sides have the same length. Is the number of vertex guards who are sometimes necessary and always sufficient to view the interior of an equilateral n-gon also ⌊n/3⌋?
2. Is the number of vertex guards who are sometimes necessary and always sufficient to view the interior of an equilateral orthogonal n-gon also ⌊n/4⌋? What numbers of sides can an equilateral orthogonal polygon have?
3. A vertex v on the boundary of a simple polygon P clearly sees a vertex w in the interior of P if the line segment from v to w contains only points in the interior of P. Clear visibility has not been widely studied and deserves more attention.
4. Often in discussions of art gallery theorems it is assumed that there are no 3 vertices of the polygon on a line or other similar types of assumptions. This type of assumption seems especially to rule out situations of interest for rectilinear polygons. What happens when such assumptions are not made?
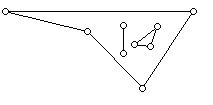
5. The problems above are stated for polygons but one can generalize these problems to allowing "holes" and free standing walls. Some of these types of problems are still open. (See the diagram below.)
Web resources related to Art Gallery Theorems:
1. http://eric.gruver.net/ArtGalleryProblems.html
2. http://citeseer.ist.psu.edu/484295.html
Note: Many articles and preprints related to art gallery problems can be found at:
http://citeseer.ist.psu.edu/
http://scholar.google.com
3. In addition to materials about art gallery theorems Godfried Toussaint's web pages have lots of wonderful preprints and applets devoted to topics in computational geometry.
http://cgm.cs.mcgill.ca/~godfried/teaching/cg-web.html#gallery
4. Not all of these problems are still unsolved but this page is worth a look anyway.
http://www.csi.uottawa.ca/~jorge/openprob/
5. http://mathworld.wolfram.com/ArtGalleryTheorem.html
http://en.wikipedia.org/wiki/Art_gallery_theorem
6. There is a nice module related to these matters that can be downloaded from the DIMACS Modules site. Look at Module 7-01
http://dimacs.rutgers.edu/Publications/Modules/moduleslist.html
7. There is a wonderful applet to compute the kernal of a simple polygon (i.e. points from which all of the polygon is is visible) and the visibility polygon of a simple polygon from a point of your choice at:
http://web.informatik.uni-bonn.de/I/GeomLab/VisPolygon/index.html.en#VisPolygon1Applet