10/28/99
Equity and Fairness Sampler
Prepared by:
Joseph Malkevitch
Mathematics and Computing Dept.
York College (CUNY)
Jamaica, New York 11451
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
Elections
The ballots below show the rankings of 55 faculty for 5 choices of textbooks. Which
book deserves to be selected as the choice for the group?
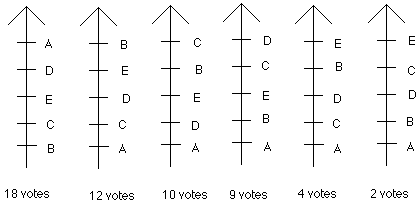
(Note: There is no indifference; higher preferences towards the top.)
Bankruptcy
There are three merchants who have
verified claims against the remaining assets of a small company. What would be a fair
way to settle the claims in each case?
Example 1:
Claimant A B C (Assets Remaining: $200)
Claim $30 $100 $100
Example 2:
Claimant A B C (Assets Remaining: $200)
Claim $30 $200 $300
Apportionment
The four divisions of a college, Arts, Sciences, Business, and Education have enrollments
of:
2,180
1,880
1,420
640
A wealthy alumna of the college has decided to donate 30 scholarships to attract new
students based on the different divisions' enrollment.
What is a fair way to assign the 30 scholarships to each division?
What would be a fair assignment if there were 31 scholarships?
Fair Division
Benjamin (B) and Alexander (A) are siblings and have each, without the input of the
other, assigned a dollar value to several items that their mother Nina has willed
to them. Each of the brothers has enough cash to make payments to the other in order
to equalize any possible division that is suggested.
A B
Turkish Rug $1100 $1800
Stamp Collection $1900 $1200
Book Collection $20000 $30000
Ethnic Jewelry $6000 $5000
What would be a fair way to handle the situation? (What would you do if the brothers
had listed the same amount for some items?)
Cost Sharing I
Towns A and B with populations of 12 and 8 (in hundreds of thousands) need to build
a new water supply system.
Stand alone costs (in millions of dollars):
{A} = 160 {B} = 90
Joint cost: {A, B} = 200
How should A and B proceed?
Cost Sharing II
Towns A, B, and C with populations of 12, 10, and 8 (in hundreds of thousands) need
to build a new water supply system.
Example 1:
Stand alone costs (in millions of dollars):
{A} = 150 {B} = 120 {C} = 90
Joint costs:
{A, B} = 240 {A, C} = 220 {B, C} = 180
{A, B, C} = 325
How should A, B, and C proceed?
Example 2:
Stand alone costs (in millions of dollars):
{A} = 150 {B} = 120 {C} = 90
Joint costs:
{A, B} = 240 {A, C} = 220 {B, C} = 180
{A, B, C} = 315
How should A, B, and C proceed?
Legislative Fairness
The five towns in Rural County have populations of 7, 4, 3, 3, and 1 (in hundreds
of thousands), respectively.
Is it fair for the representatives of these 5 towns to cast 7, 4, 3, 3, and 1 vote,
respectively, where 10 votes are required to take action in the county legislature?
Games
Players named Row and Column independently choose a row (choice of two) and column
(choice of two), respectively. The "payoff" is shown in the cell at the intersection
of the chosen row/column pair. The payoffs shown are from Row's point of view. Column's payoff is the negative of the number shown.
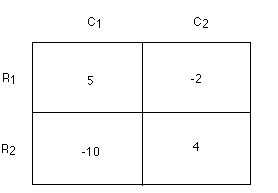
Is this a fair game?
How should Row and Column play the game to achieve his/her best result if the game
is played:
a. Once?
b. Many times?
Transplants
Which of these factors should be taken into account in deciding whether or not someone
is a suitable candidate for a transplant?
How famous the patient is?
How wealthy the patient is?
How old the patient is?
How sick the patient is?
How long the patient has been waiting for a transplant?
Things to consider:
1. What principles of fairness and equity do you think are essential in dealing with
the situations above?
2. If everyone is "happy" with the way the situation is resolved does this mean the
solution method is a "good" one?
3. In some of the situations above the participants had some freedom to "lie" about
some of the information provided. What are the consequences of this possibility?
4. What issues arise if, after a solution is effected, additional information becomes
available (e.g. in the bankruptcy situation perhaps: a. Another creditor appears;
b. more assets are available than originally thought)?
5. Can you think of situations where being fair is not the only concern in attempting
to deal with the situations?
Equity and Fairness Questions and Projects
1. How would one measure whether the distribution of income (or wealth) is more equitable
in one country than in another?
2. How can one compare the fairness (equitability) of different tax systems?
3. In English, the words "fair" and "equitable" have somewhat different connotations.
What are their differences? Can a procedure be "fair" but not "equitable?" Can a
procedure be "equitable" but not "fair?"
4. For different areas of knowledge (e.g. accounting, medicine, business) can you
find examples of situations where being fair and equitable are matters of concern?
5. Discuss how one can design fair election districts?
Short list of most important references:
Aumann, R. and S. Hart (Eds.) Handbook of Game Theory with Economic Applications,
North-Holland, New York, Volume 1, (1992), Volume 2, (1994).
Balinski, M. and H.P. Young, Fair Representation, Yale University Press, New Haven,
1982.
Brams, S. and A. Taylor, Fair Division, Cambridge U. Press, New York, 1996.
Kuhn, H. (ed.), Classics in Game Theory, Princeton U. Press, Princeton, 1997.
Mc Lean, I. and A. Urken, Classics of Social Choice, U. Michigan Press, Ann Arbor,
1995.
Moulin, H., Axioms of Cooperative Decision Making, Cambridge U. Press, New York, 1988.
Robinson, J. and W. Webb, Cake-Cutting Algorithms, A K Peters, Natick, 1998.
Saari, D., Geometry of Voting, Springer-Verlag, New York, 1994.
Straffin, P., Game Theory and Strategy, Mathematical Association of America, Washington,
1993.
Taylor, A., Mathematics and Politics, Springer-Verlag, New York, 1995.
Young, H.P. (Ed.), Fair Allocation, American Mathematical Society, Providence, 1985.
Young, H.P., Equity, Princeton U. Press, Princeton, 1994.
Acknowledgements:
1. National Science Foundation
2. Long Island Consortium for Interconnected Learning (administered by SUNY Stony
Brook)
Director: Alan Tucker (Applied Mathematics)
3. York College (City University of New York)
Return to Joseph Malkevitch's Home Page

